PRACA ORYGINALNA
Bending of the three-span rail (UIC 60) subjected to the concentrated force
1
Politechnika Poznańska, Instytut Mechaniki Stosowanej, Polska
2
Łukasiewicz Research Network, Poznan Institute of Technology, Polska
Data nadesłania: 20-08-2025
Data ostatniej rewizji: 18-09-2025
Data akceptacji: 27-09-2025
Data publikacji online: 13-10-2025
Data publikacji: 13-10-2025
Rail Vehicles/Pojazdy Szynowe 2025,1-2,32-38
SŁOWA KLUCZOWE
DZIEDZINY
STRESZCZENIE
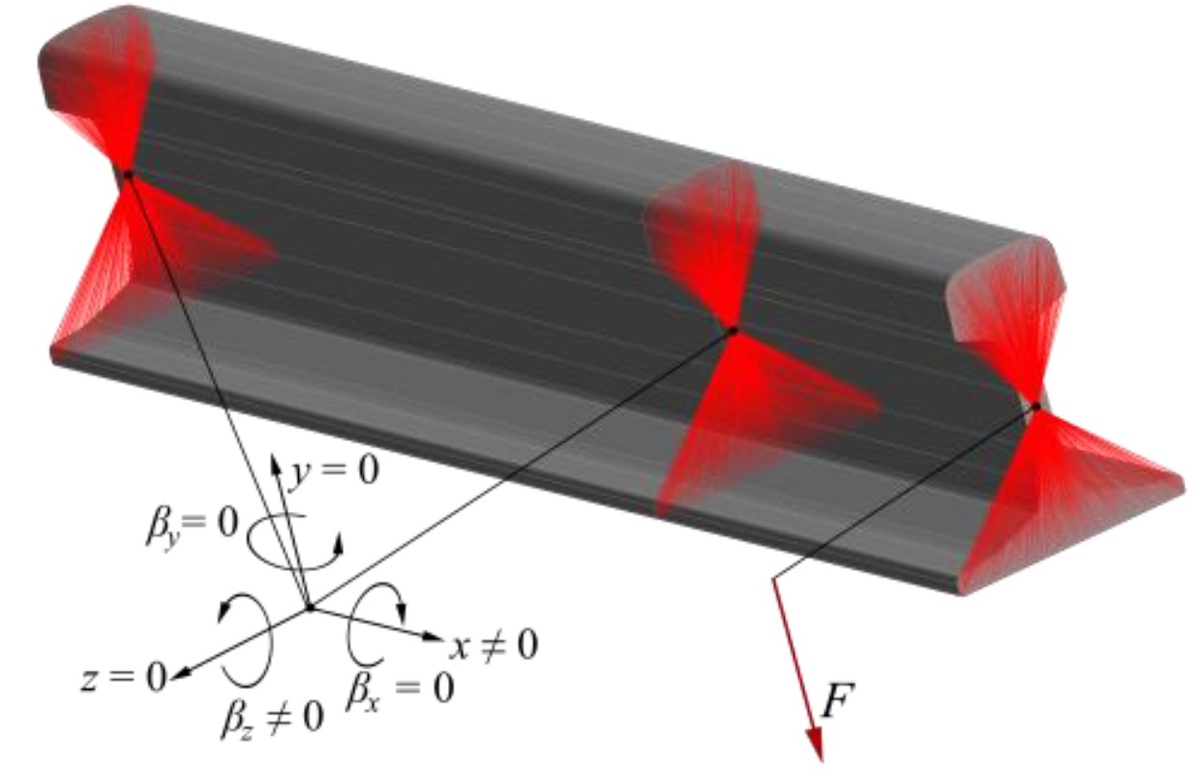
The subject of the paper is the three-span rail (UIC 60) simply supported on four sleepers. The middle span is subject to the concentrated force at half of its length. Analytical study of the bending problem of the three parts of this rail is realized with consideration of the Timoshenko beam theory. Moreover, the bending problem is studied numerically using the finite element method (FEM). Based on the obtained analytical results it is seen that structures like rails should be analysed with shear effect taking into account. The result obtained this way is consistent with the results of numerical investigation. Ignoring the shear effect results in a significant underestimation of the deflection.
REFERENCJE (16)
1.
Afridi AH, Zhu H, Camacho ET, Deng G, Li H. Numerical modeling of rolling contact fatigue cracks in the railhead. Eng Fail Anal Part B. 2023;143:106838. https://doi.org/10.1016/j.engf....
2.
Ahmed AM, Rifai AM. Euler-Bernoulli and Timoshenko beam theories analytical and numerical comprehensive revision. European J Engineer Tech Res. 2021;6(7):20-32. https://doi.org/10.24018/ejers....
3.
Camille C, Mirza O, Kirkland B, Clarke T. Structural behaviour of prestressed concrete sleepers reinforced with high-performance macro synthetic fibres. Eng Fail Anal. 2022;141:106671. https://doi.org/10.1016/j.engf....
4.
Gere JM, Timoshenko SP. Mechanics of materials. PWS-KENT Publishing Company: Boston 1984.
5.
Gharawi MA, Saadoon AM, Hmoad NR, Albayati AH. Structural performance of rail connections: experimental testing and finite element modelling. Results Eng. 2025;27:105997. https://doi.org/10.1016/j.rine....
6.
He C, Yang Z, Zhang P, Li S, Naeimi M, Dollevoet R et al. A finite element thermomechanical analysis of the development of wheel polygonal wear. Tribol Int. 2024;195:109577. https://doi.org/10.1016/j.trib....
7.
Hutchinson JR. Shear coefficient for Timoshenko beam theory. ASME J Applied Mech. 2001;68:87-92. https://doi.org/10.1115/1.1349....
8.
Katili I, Syahril T, Katili AM. Static and free vibration analysis of FGM beam based on unified and integrated of Timoshenko’s theory. Compos Struct. 2020;242:112130. https://doi.org/10.1016/j.comp....
9.
Kennedy GJ, Hansen JS, Martins JRRA. A Timoshenko beam theory with pressure corrections for layered orthotropic beams. 2011;48:2373-2382. https://doi.org/10.1016/j.apm.....
10.
Knuth C, Squicciarini G, Thompson D. An efficient model for predicting the sound radiation from a railway rail accounting for cross-section deformation. J Sound Vib. 2025;618, Part B:119323. https://doi.org/10.1016/j.jsv.....
11.
Nampally P, Reddy JN. Geometrically nonlinear Euler–Bernoulli and Timoshenko micropolar beam theories. Acta Mechanica. 2020;231:4217-4242. https://doi.org/10.1007/s00707....
12.
Romanoff J, Reddy JN. Experimental validation of the modified couple stress Timoshenko beam theory for web-core sandwich panels. Compos Struct. 2014;111:130-137. https://doi.org/10.1016/j.comp....
13.
Roque CMC, Fidalgo DS, Ferreira AJM, Reddy JN. A study of a microstructure-dependent composite laminated Timoshenko beam using a modified couple stress theory and a meshless method. Compos Struct. 2013;96:532-537. https://doi.org/10.1016/j.comp....
14.
Timoshenko SP. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Philosophical Magazine. 1921;41:744-746.
15.
Wang YQ, Liang C, Zu JW. Examining wave propagation characteristics in metal foam beams: Euler–Bernoulli and Timoshenko models. J Brazilian Society Mech Sciences Engineering 2018;40:565. https://doi.org/10.1007/s40430....
16.
Wang CM, Reddy JN, Lee KH. Shear deformable beams and plates. Relationships with classical solutions. Amsterdam, Lausanne, New York, Oxford, Shannon, Singapore, Tokyo 2000.
Udostępnij
ARTYKUŁ POWIĄZANY
Przetwarzamy dane osobowe zbierane podczas odwiedzania serwisu. Realizacja funkcji pozyskiwania informacji o użytkownikach i ich zachowaniu odbywa się poprzez dobrowolnie wprowadzone w formularzach informacje oraz zapisywanie w urządzeniach końcowych plików cookies (tzw. ciasteczka). Dane, w tym pliki cookies, wykorzystywane są w celu realizacji usług, zapewnienia wygodnego korzystania ze strony oraz w celu monitorowania ruchu zgodnie z Polityką prywatności. Dane są także zbierane i przetwarzane przez narzędzie Google Analytics (więcej).
Możesz zmienić ustawienia cookies w swojej przeglądarce. Ograniczenie stosowania plików cookies w konfiguracji przeglądarki może wpłynąć na niektóre funkcjonalności dostępne na stronie.
Możesz zmienić ustawienia cookies w swojej przeglądarce. Ograniczenie stosowania plików cookies w konfiguracji przeglądarki może wpłynąć na niektóre funkcjonalności dostępne na stronie.